What is a CI?

• Using a Statistic to estimate a Parameter

• It is NOT a probability

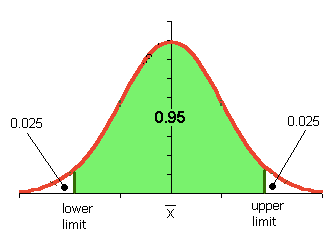
• It is an interval that will cover the true parameter X% of the time

  

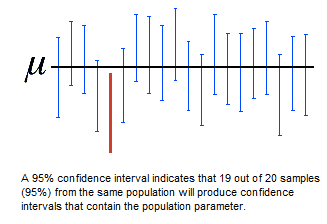
• So we can interpret a CI as

  • "We are X% confident that the true population parameter lies within A and B"

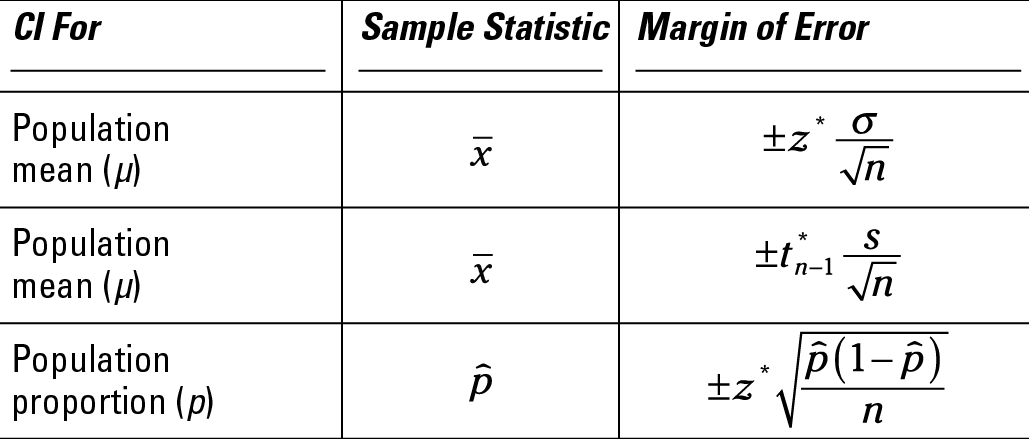
General Math Behind a CI

• Formula

  • Point Estimate ± Margin of Error

  • Point Estimate ± Critical Value * Standard Error

  

• Point Estimate

  

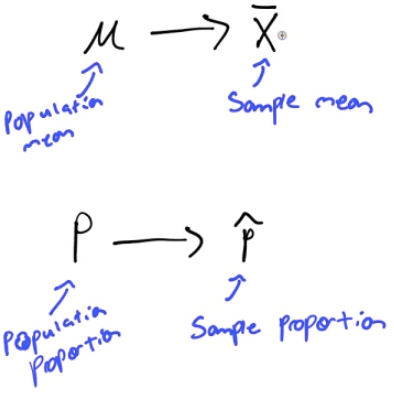
• Critical Value

  

  

• Standard Error

  

  

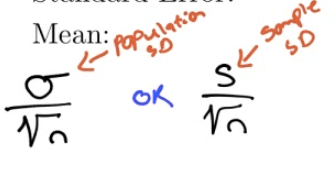
• Confidence Interval

  

Steps to Calculating a CI

• Read the problem and outline the STASTICS

• Check your CONDITIONS

  • Random

  • Independent: N≥10n

  • Normal: n>30

• CALCULATE

  • Point Estimate ± Critical Value * Standard Error

• INTERPRET

• Some Can Calculate Intervals

Practice Questions

1. The effect of drugs and alcohol on the nervous system have been the subject of considerable research. Suppose a neurologist is testing the effect of a drug on response time by injecting 50 rats with a dose, subjecting each to a stimulus, and recording the response time. The average response time for the 50 injected rats was 1.26s. Assuming the mean response time for a rat that has not been injected with the drug is 1.4s with standard deviation of 0.45, construct a 90% confidence interval to determine if the drug has an effect on response time.

   • Statistics

     • Mean = 1.26

     • Population SD = 0.45

     • n = 50

     • CL = 90%

   • Conditions

     • Random: Assume rats are a random sample

     • Independent: N > 10n

     • Normal: n > 50

   • Calculate

   

   

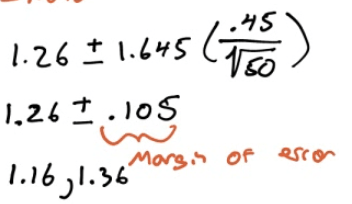
   • Calculate by calculator

   

   

   

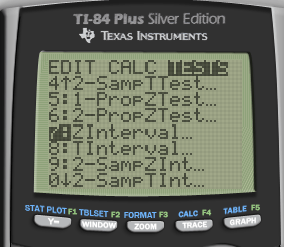
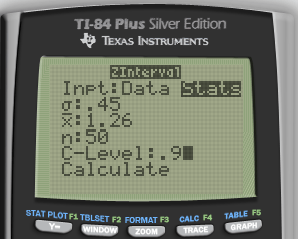
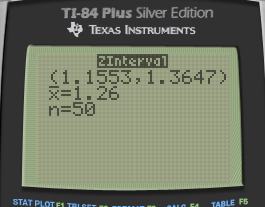
   • Calculated using Z test

• Interpret

  • We are 90% confident that the true mean response time for rats given the new drug is between 1.16s and 1.36s.

  • 1.4s is not in the interval, so we have evidence the new drug make rats faster

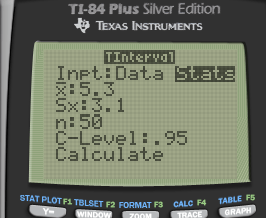
1. There are two fire stations in a town, one in the northern half and one the southern half. The one in the northern part is known to respond to calls within 4 min. The council members in the town are worried that the southern fire station isn’t as good so they hire a statistician. The statistician collects a random sample of 50 call/responses from the southern fire station. The mean response time is 5.3 min with a standard deviation of 3.1. Construct a 95% confidence interval to determine if the council members have cause to worry about the southern station

   • Statistics

     • Mean = 3.5

     • Sample SD = 3.1

     • n = 50

     • CL = 95%

   • Conditions

     • Random: Yes

     • Independent: N > 10n = 500

     • Normal: n > 30

   • Calculate

   

   

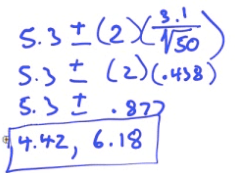
   • Calculate by calculator

   

   

   

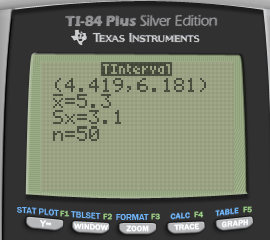
   • Interoperate

     • We are 95% confident that the true population mean response time for the southern fire station is between 4.42 and 6.18 mins

     • 4 is not in the interval, so we do have reason to be concerned.

1. The US Department of Transportation reported that 75% of all fatally injured automobile drivers were intoxicated. A random sample of 32 records in Carson County, Colorado, showed that 16 involved a drunk driver. Use a 99% confidence interval to determine whether or not there is evidence that indicates the population proportion of driver fatalities related to alcohol is different than 75%

   • Statistics

     • P hat = x / n = 16/32 = 0.5

     • n = 32

     • CL = 99%

   • Conditions

     • Random: Yes

     • Independent: N > 10n = 320

     • Normal: n * p hat > 10 and n * (1-p hat) >10

   • Calculate

   

   

   • Calculate by calculator

   

   

   

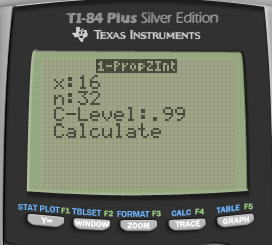
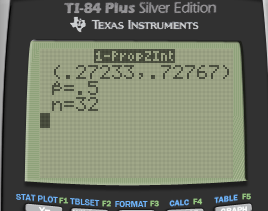
   • Interperate

     • We are 99% confident that the true population proportion of driver fatalties in Carson County is between 27.2% and 72.8%

     • 75% is not in our interval, so it appears that Carson County is lower in the US